Notes for EHT01 at INI:
Attention: these notes are unfaithful and perhaps contains some unoriginal remarks (=remarks made by myself).
ClICK HERE TO EXPAND
- Clark Barwick
- Spectral Mackey functors &
-categorical approaches to equivariant homotopy theory
- Spectral Mackey functors &
- Clover May
- Mackey functors in equivariant homotopy theory
- Modules of equivariant EM spectra
- Emanuele Dotto
- An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Foling Zhou (untaken)
- A
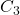-equivariant computation of tmf
- A
- Jeremy Hahn
- A biased view of equivariant stable homotopy theory
- The prismatization of complex bordism
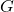-compact group (incomplete)
- Lennart Meier
- Topological modular forms and bilinear forms I & II (incomplete)
- Markus Hausmann (untaken)
- Equivariant Thom spectra I & II
- Michael Hill
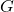- -Commutative monoids
- Stability in an unstable world
- Mona Merling
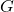- -Manifolds and equivariant homotopy theory
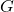- -Manifolds and equivariant
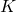-theory
- Teena Gerhardt
- THH, Witt vectors and equivariance
- Vesna Stojanoska
- Introduction to chromatic homotopy theory
- Chromatic homotopy theory today (untaken)
Notes for Real algebraic -theory and trace methods in Paris (highly incomplete) :
To be uploaded.
Notes taken regarding 
(thanks to Prof. Thomas Nikolaus and Prof. Achim Krause） :
ClICK HERE TO EXPAND
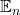-Algebra- Tate
- Tate Diagonal
- Hochschild Homology
- Connes Operator
- Cyclic Homology and Periodic Homology
- HKR and the Cotangent Complex
- The Cotangent Complex and Obstruction Theory
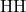of Schemes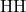- in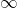
-Categories - Bökstedt Periodicity
- Properties of
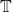-Action on 
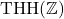
- Negative Topological Cyclic Homology
- Topological Periodic Homology
- The Cyclotomic Structure
- Topological Cyclic Homology
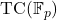
- of Perfect Rings
- Frobenius Lifts and Group Rings
Notes taken regarding the paper On the nonexistence of elements of Kervaire invariant one (and simultaneously Adams spectral sequence):
This will be a fruitful “project”. See here.
Miscellaneous:
A brief note of 
-theory and GW spectra based majorly on a Münster lecture given by Yonatan Harpaz and Markus Land.